Guía completa para calcular y aplicar ángulos de elevación y depresión

Si te encuentras en la necesidad de calcular el ángulo de elevación o depresión, es importante que conozcas los pasos necesarios para llevar a cabo esta tarea. Este proceso es fundamental en diferentes ámbitos, desde la construcción de edificios hasta la medición de la altura de un objeto o la distancia a la que se encuentra.

Para calcular el ángulo de elevación o depresión, es necesario que conozcas la altura del objeto que deseas medir y la distancia a la que te encuentras de él. A partir de esta información, puedes utilizar la trigonometría para obtener el ángulo deseado.

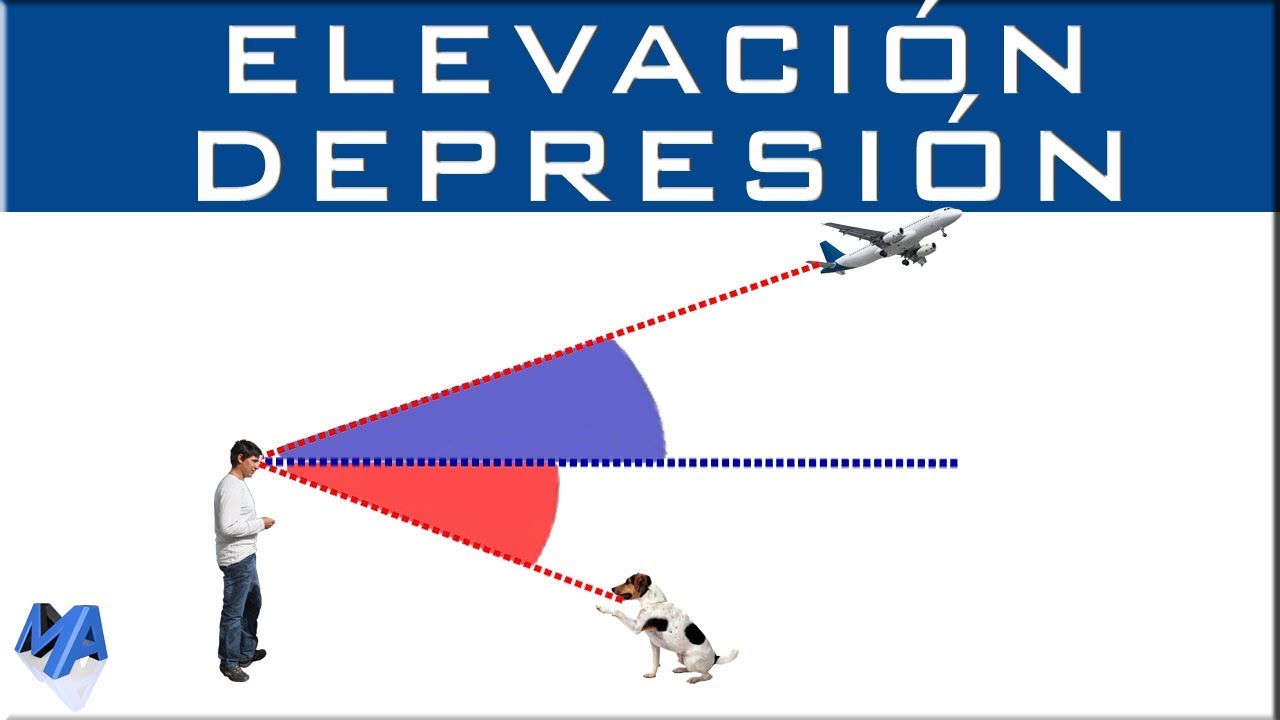
El ángulo de elevación se refiere al ángulo que se forma entre la línea de visión y la horizontal, mientras que el ángulo de depresión se refiere al ángulo que se forma entre la línea de visión y la vertical. Conocer estos conceptos te permitirá llevar a cabo el cálculo de manera más precisa y eficiente.

Cómo calcular el ángulo de elevación y depresión

Cuando se trata de medir la altura de un objeto o la profundidad de un agujero, es necesario conocer el ángulo de elevación o depresión. Estos conceptos son fundamentales en la trigonometría y se utilizan en diversas áreas como la arquitectura, la ingeniería y la topografía.

Cálculo del ángulo de elevación

El ángulo de elevación se refiere al ángulo que forma la línea de visión con la horizontal, es decir, la inclinación hacia arriba desde el punto de observación. Para calcularlo, se debe seguir los siguientes pasos:

1. Identificar el objeto que se desea medir y el punto de observación.
2. Medir la distancia horizontal entre el objeto y el punto de observación.
3. Medir la altura del objeto desde su base hasta la parte superior.
4. Aplicar la fórmula: ángulo de elevación = arcotangente (altura del objeto / distancia horizontal).

Los valores de altura y distancia deben estar en la misma unidad de medida para obtener resultados precisos.

Cálculo del ángulo de depresión

El ángulo de depresión, por otro lado, es el ángulo que forma la línea de visión con la horizontal hacia abajo, es decir, la inclinación hacia abajo desde el punto de observación. Para calcularlo, se deben seguir los siguientes pasos:

1. Identificar el objeto que se desea medir y el punto de observación.
2. Medir la distancia horizontal entre el objeto y el punto de observación.
3. Medir la profundidad del objeto desde su base hasta la parte inferior.
4. Aplicar la fórmula: ángulo de depresión = arcotangente (profundidad del objeto / distancia horizontal).

En ambos casos, es necesario tener en cuenta que el ángulo de elevación o depresión puede variar según el punto de observación y la posición del objeto. Es recomendable realizar varias mediciones desde diferentes puntos para obtener una medida más precisa.

Fórmulas para calcular el ángulo de elevación y depresión

Si alguna vez has necesitado calcular el ángulo de elevación o depresión en un proyecto, sabrás que no siempre es fácil. Pero no te preocupes, aquí te explicamos las fórmulas que necesitas para hacerlo.

Ángulo de elevación

Para calcular el ángulo de elevación, debes seguir los siguientes pasos:

1. Medir la distancia horizontal entre el punto de observación y el objeto que se quiere medir.
2. Medir la altura del objeto desde su base hasta la parte superior.
3. Usar la fórmula: ángulo = arctan (altura/distancia)

Ángulo de depresión

Para calcular el ángulo de depresión, debes seguir los siguientes pasos:

1. Medir la distancia horizontal entre el punto de observación y el objeto que se quiere medir.
2. Medir la altura del punto de observación desde la base hasta el suelo.
3. Medir la altura del objeto desde su base hasta la parte inferior.
4. Usar la fórmula: ángulo = arctan ((altura del punto de observación – altura del objeto)/distancia)

Para usar estas fórmulas necesitas conocer la trigonometría básica y tener una calculadora científica a mano.

Si quieres ver un ejemplo práctico de cómo se aplican estas fórmulas, te recomendamos que veas el siguiente vídeo. ¡Te sorprenderá lo fácil que es una vez que lo ves en acción!

Y recuerda, siempre es importante tener en cuenta el ángulo de elevación o depresión en proyectos como la construcción de edificios, puentes o incluso en la fotografía. ¡No subestimes su importancia!

Uso de la trigonometría para calcular ángulos de elevación y depresión

La trigonometría es una rama de las matemáticas que se enfoca en el estudio de las relaciones entre los lados y los ángulos de los triángulos. Esta ciencia tiene una gran cantidad de aplicaciones en la vida cotidiana, y una de ellas es el cálculo de ángulos de elevación y depresión.

¿Qué son los ángulos de elevación y depresión?

Los ángulos de elevación y depresión son medidas angulares que se utilizan para determinar la altura de un objeto en relación con un observador. El ángulo de elevación se refiere al ángulo que forma la línea de visión del observador con la horizontal, mientras que el ángulo de depresión se refiere al ángulo que forma la línea de visión con la vertical.

¿Cómo se calculan los ángulos de elevación y depresión?

Para calcular los ángulos de elevación y depresión se requiere el uso de la trigonometría. En primer lugar, se debe identificar el triángulo que se forma entre el observador, el objeto y la línea de visión. A continuación, se pueden utilizar las funciones trigonométricas del seno, coseno y tangente para calcular los ángulos y las longitudes de los lados del triángulo.

Por ejemplo, si se sabe la distancia entre el observador y el objeto, se puede utilizar la tangente para calcular el ángulo de elevación o depresión. La fórmula es la siguiente:

tangente del ángulo = altura del objeto / distancia al objeto

También se pueden utilizar otras fórmulas, como la ley de los senos o la ley de los cosenos, dependiendo de la información disponible y el tipo de triángulo que se esté analizando.

Aplicaciones de los ángulos de elevación y depresión

Los ángulos de elevación y depresión tienen una gran cantidad de aplicaciones prácticas. Por ejemplo, se utilizan en la construcción de edificios y puentes para determinar las alturas y las inclinaciones de las estructuras. También se utilizan en la navegación aérea y marítima para calcular la altura de los aviones o barcos en relación con el nivel del mar.

Guía completa para calcular y aplicar ángulos de elevación y depresión

Si estás interesado en la topografía o en la construcción, es probable que hayas oído hablar de los ángulos de elevación y depresión. Estos términos se refieren a la medida del ángulo entre la línea de visión y la horizontal, y son fundamentales para determinar la altura de un objeto o la profundidad de una excavación. En esta guía, te explicaremos todo lo que necesitas saber sobre cómo calcular y aplicar ángulos de elevación y depresión.

¿Qué es un ángulo de elevación?

Un ángulo de elevación es el ángulo formado por la línea de visión y la horizontal cuando el objeto observado está por encima del nivel del observador. Para calcular el ángulo de elevación, es necesario medir la altura del objeto y la distancia horizontal entre el objeto y el observador. A continuación, se puede utilizar la trigonometría para calcular el ángulo.

¿Qué es un ángulo de depresión?

Un ángulo de depresión es el ángulo formado por la línea de visión y la horizontal cuando el objeto observado está por debajo del nivel del observador. Para calcular el ángulo de depresión, es necesario medir la altura del observador y la distancia horizontal entre el objeto y el observador. A continuación, se puede utilizar la trigonometría para calcular el ángulo.

¿Cómo se aplican los ángulos de elevación y depresión?

Los ángulos de elevación y depresión son fundamentales en la topografía y la construcción. Por ejemplo, en la construcción de un edificio, es necesario calcular los ángulos de elevación y depresión para determinar la altura de los pisos y la profundidad de las excavaciones. En la topografía, los ángulos de elevación y depresión se utilizan para medir la altura de los objetos y la profundidad de las excavaciones.

Preguntas frecuentes sobre cómo calcular el ángulo de elevación y depresión

¿Te has preguntado alguna vez cómo calcular el ángulo de elevación y depresión? Si eres un aficionado a la astronomía, la topografía o la navegación, seguramente te hayas enfrentado a esta cuestión alguna vez. En esta sección de preguntas frecuentes, encontrarás respuestas a las dudas más comunes sobre cómo medir estos ángulos y cómo aplicarlos en diferentes situaciones. No te pierdas esta guía práctica para dominar el cálculo de ángulos de elevación y depresión.

¿Cuál es la fórmula matemática precisa para calcular el ángulo de elevación o depresión en un problema de trigonometría avanzada?

La fórmula matemática precisa para calcular el ángulo de elevación o depresión en un problema de trigonometría avanzada es:

• Para el ángulo de elevación: ángulo = arctan(opuesto/adyacente)
• Para el ángulo de depresión: ángulo = 90° – arctan(opuesto/adyacente)

Es importante recordar que:

• El ángulo se mide en grados.
• El opuesto es la altura del objeto que se está observando desde el punto de vista del observador.
• El adyacente es la distancia horizontal entre el objeto y el observador.

¿Cómo puedo calcular el ángulo de elevación o depresión de un objeto utilizando trigonometría?

Para calcular el ángulo de elevación o depresión de un objeto utilizando trigonometría, debemos conocer la distancia horizontal entre el observador y el objeto, así como la altura del observador y la altura del objeto. Luego, podemos utilizar la función tangente para obtener el ángulo deseado. La fórmula sería: ángulo = arctan (altura del objeto – altura del observador / distancia horizontal). El ángulo de elevación se mide desde el suelo hacia arriba, mientras que el ángulo de depresión se mide desde el cielo hacia abajo.